Matemática

Expressões matemáticas

Quando você quer escrever alguma coisa matemática, que pode ser uma equação ou uma simples variável, você deve colocar \( para iniciar a expressão matemática e \) para fechá-la.

\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage[T1]{fontenc}

\begin{document}
	Exemplos de expressões matemáticas: \( x \) e \( x + y = 3 \)
\end{document}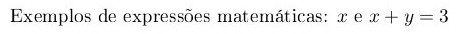

Percebam que, dessa forma, as expressões matemáticas ficam inline, ou seja, na mesma linha do restante do texto.

Se você quiser escrever alguma coisa que fique em destaque, em uma linha própria e centralizado, você pode escrever \[ para iniciar a expressão matemática e \] para fechá-la:

\[x + y  = 7\]
\[2x - y = 5\]

Não coloque coisas que não forem matemáticas, dentro de comandos de expressões matemáticas.

Errado: \(x e y\)

Certo: \(x\) e \(y\)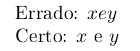

Se você quiser usar texto dentro de uma expressão matemática, use comandos de fontes específicos para uso em expressões matemáticas. Exemplo:

\(x\ \mathrm{e}\ y\)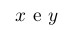

Note a necessidade do uso da barra invertida para que os espaços sejam impressos.

Você pode querer numerar expressões matemáticas que ficam em destaque, para que você possa referenciá-las. Para fazer isso, use o ambiente equation, colocando nele a expressão e um nome para ela no \label.

\begin{equation}
  x + 5 = 3
  \label{equacao-polinomial-do-primeiro-grau}
\end{equation}

\begin{equation}
  x^2 -5x + 6 = 0
  \label{equacao-polinomial-do-segundo-grau}
\end{equation}

Para referenciar a expressão, é só usar o comando \ref{label-da-expressao}. Se você já viu o tutorial de referências cruzadas, vai entender facilmente, pois a lógica é a mesma. Exemplo:

Nesse documento, temos uma equação polinomial do 1º grau
(\ref{equacao-polinomial-do-primeiro-grau}) e uma equação polinomial do 2º grau
(\ref{equacao-polinomial-do-segundo-grau}).

Funções matemáticas

No LaTeX, quando você quiser escrever alguma função matemática, como log de logaritmo, e tan, de tangente, não escreva simplesmente log ou tan.

O LaTeX vai entender que cada letra é uma variável e que você está escrevendo um produto delas. Ao invés disso, use o comando da função (no caso, \log e \tan):

Logaritmo: \( \log_28 = 3 \)

Tangente: \( \tan 45^\circ = 1 \)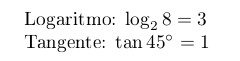

O underline serve para colocar um subscript, que é simplesmente algo que fica abaixo do texto que fica ao lado dele. O acento circunflexo serve para colocar um superscript, que é o contrário do subscript, ou seja, fica acima do texto que fica ao lado dele.

O símbolo do grau é impresso combinando o superscript com o comando \circ. Isso é útil em comandos como o \tan e o \sec (para secante):

Secante: \( \sec 60^\circ = 2 \)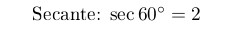

Símbolos matemáticos

Você pode precisar colocar símbolos matemáticos no seu documento. O LaTeX é muito completo quando o assunto é Matemática, então é muito difícil você não encontrar o símbolo que você precisa.

Vale lembrar que o LaTeX também tem bons pacotes para outras áreas de Ciências Exatas, como Química e Física. Veja na imagem abaixo uma pequena parte dos símbolos cobertos pelo LaTeX:

Você pode encontrar muito mais símbolos aqui.

Unidades

Considere a marcação abaixo:

\( 10m \)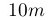

Se você escrever 10m, querendo dizer 10 vezes uma variável chamada m, ok, mas se você quer dizer 10 metros, então coloque o m com uma fonte romana usando o comando \mathrm e dê um espaço entre o 10 e o m usando \,:

\( 10\,\mathrm{m} \)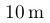

Delimitadores

É comum que você queira usar delimitadores ao escrever um documento matemático. Para colocar parênteses, não há segredo: simplesmente coloque a expressão dentro de parênteses.

\( (x + 2) \div 2 = 7 \)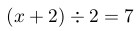

A altura dos delimitadores pode não bater com a altura da expressão envolvida:

\( (\frac{x^2}{y^3}) \)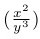

Para corrigir isso, é só colocar \left antes do primeiro delimitador e \right antes do segundo:

\( \left(\frac{x^2}{y^3}\right) \)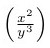

Há outros delimitadores:

Colchetes:\newline

\( \left[\frac{x^2}{y^3}\right] \)\newline

Chaves:\newline

\( \left\{\frac{x^2}{y^3}\right\} \)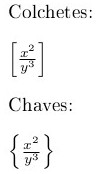

Note que as chaves precisam ser escapadas.

Matrizes

Para criar matrizes, use o ambiente array:

\[
  A = \left(
    \begin{array}{cc}
      13 & 7 \\
      4  & 9
    \end{array}
  \right)
\]

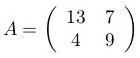
O argumento obrigatório é a estrutura da array. Cada caractere representa uma coluna. O caractere 'c' quer dizer que a coluna ficará centralizada. O & é usado para separar colunas. Usa-se \\ para finalizar linhas. A sintaxe é a mesma das tabelas, cobertas no tutorial de tabelas.

Teoremas

O LaTeX tem um comando especial para definir tipos de teoremas: \newtheorem. Ele tem dois argumentos obrigatórios. O primeiro é o nome do ambiente para criar o teorema e o segundo é o nome que os teoremas desse tipo receberão.

\newtheorem{teorematrigonometria}{Teorema}

Para criar um novo teorema do tipo informado, é só criar um novo ambiente com o mesmo tipo:

\begin{teorematrigonometria}
  O quadrado da hipotenusa é igual à soma dos quadrados dos catetos:

  \( c^2 = a^2 + b^2 \)
\end{teorematrigonometria}

Quando você cria teoremas, você pode fazer com que eles sigam a numeração de alguma outra estrutura, que pode ser, por exemplo, uma seção, um capítulo ou outro teorema. Apenas para demonstrar isso, será criado um novo tipo de teorema:

\newtheorem{teoremaaritmetica}{Teorema}

Também será criado um teorema desse tipo, o Teorema fundamental da Aritmética, com esse novo tipo:

\begin{teoremaaritmetica}
  O Teorema Fundamental da Aritmética sustenta que todos os números inteiros positivos maiores que 1 podem ser
  decompostos num produto de números primos, sendo esta decomposição única a menos de permutações dos fatores.
\end{teoremaaritmetica}

Perceba que o segundo teorema tem a sua própria numeração. Para fazer com que ele siga a numeração de outro tipo de teorema, deve-se passar o tipo do teorema como argumento opcional:

\newtheorem{teoremaaritmetica}[teorematrigonometria]{Teorema}

Se o objetivo for fazer com que o teorema siga a numeração de uma estrutura, como uma seção, deve-se passar o nome da estrutura:

\newtheorem{teoremaaritmetica}[section]{Teorema}

Índices e expoentes

Índices seguem o modelo: expressao_{indice}. Se o índice tem apenas um caractere, não é necessário colocar as chaves:

Índices: \(x_1 = 3 \) e \(x_{12} = 7 \)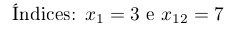

Expoentes seguem o modelo: expressao^{indice}. Eles funcionam da mesma forma que os índices. Então, se o expoente tem apenas um caractere, não é necessário colocar chaves.

Expoentes: \( x^2 \) e \( x^{3y} \)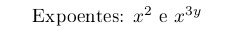

Dá pra aninhar tanto índices, quanto expoentes:

Aninhando índices e expoentes: \(x_{1_2} = 7 \), \(x^2_{1_2} = 7 \) e \(x^{y^2}\)

Raízes

Para usar raízes, basta usar o comando \sqrt passando o radicando como argumento obrigatório, e, opcionalmente, o índice (se o índice não for especificado, será usado o índice 2):

Raízes: \(\sqrt{9} = 3\) e \(\sqrt[3]{8} = 2\)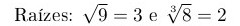

Também dá para aninhar raízes:

\(\sqrt[3]{\sqrt{64}} = 2\)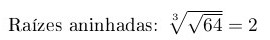

Frações

Para colocar frações, o comando é o \frac, que tem como argumentos obrigatórios, respectivamente, o numerador e o denominador da fração.

Frações: \(\frac{x + y^2}{3} \) e \(\frac{x + 4}{2}\)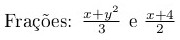

Também dá para aninhar frações:

\(\frac{\frac{2}{5} + 2}{2}\)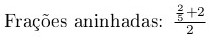

Note que a fração \(\frac{2}{5}\) ficou muito pequena. Isso aconteceu porque os parênteses são usados para expressões inline. Por isso, é melhor imprimir essa fração de forma destacada, o que aumenta bastante o tamanho dela.

Isso pode ser feito substituindo os parênteses pelos colchetes:

\[
  \frac{\frac{2}{5} + 2}{2}
\]

\[
  \frac{x + 4}{2}
\]

Fontes matemáticas

Às vezes, você pode precisar incluir texto em uma expressão matemática, ou formatar um símbolo com uma fonte diferente. Há comandos de fontes específicos para o modo matemático que você pode usar para isso:

\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage[T1]{fontenc}
\usepackage[brazilian]{babel}
\usepackage{amsfonts} % necessário para o comando \mathbb
\usepackage{bbm} % necessário para o comando \mathbbm
\usepackage{booktabs} % necessário para traçar as linhas da tabela com \toprule, \midrule e \bottomrule

\begin{document}
  \begin{center}
    \begin{tabular}{ll}
      \toprule[1.5pt]
      Fonte              & Exemplo \\
      \midrule[0.5pt]
      \verb|\mathrm|     & \(\mathrm{texto}\) \\
      \verb|\mathit|     & \(\mathit{texto}\) \\
      \verb|\mathsf|     & \(\mathsf{texto}\) \\
      \verb|\mathbb|     & \(\mathbb{A}\) \\
      \verb|\mathbbm|    & \(\mathbbm{R}\), \(\mathbbm{I}\), \(\mathbbm{N}\) e \(\mathbbm{Q}\) \\
      \verb|\mathnormal| & \(\mathnormal{texto}\) \\
      \bottomrule[1.5pt]
    \end{tabular}
  \end{center}
\end{document}

Você pode não ter o pacote bbm instalado, usado no exemplo acima. Se você estiver no Ubuntu, rode o comando abaixo para instalar esse pacote:

sudo apt-get install texlive-fonts-extra

Se você estiver no Windows, usando o MikTeX, é só instalar os pacotes que forem solicitados.

Gather e align

O pacote amsmath adiciona muitas funcionalidades matemáticas ao LaTeX que ele não suporta nativamente. Uma delas é o fornecimento de ambientes para formatar múltiplas expressões matemáticas dentro do mesmo ambiente.

Dois ambientes muito usados são o gather e o align. A diferença entre eles é que o segundo permite alinhar expressões em um caractere qualquer. Ambos usam \\ para quebrar uma linha. Veja como um sistema de equações é representado nos dois:

\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage[T1]{fontenc}
\usepackage[brazilian]{babel}
\usepackage{amsmath} % não esqueça do pacote amsmath

\begin{document}
  Sistemas de equações usando ``gather'' e ``align'':

  \begin{gather}
    2x + 3y = 16 \\
    x - y = 3
  \end{gather}

  \begin{align}
    2x + 3y &= 16 \\
    x - y &= 3
  \end{align}
\end{document}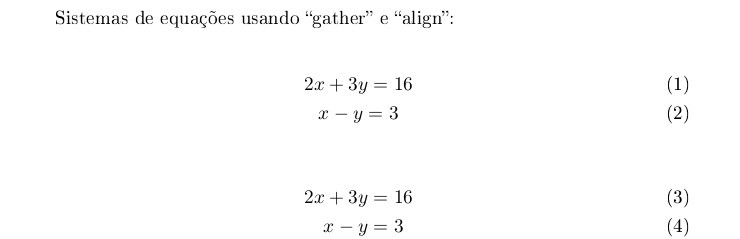

Note que as equações do segundo sistema ficaram alinhadas no sinal de igual. No ambiente align, dá para fazer isso apenas precedendo o caractere que se quer usar no alinhamento com &, como foi feito.

Pode ser que você não queira a numeração que é atribuída automaticamente em alguma das equações. Para retirá-la, basta usar o comando \notag antes de usar o comando \\ para passar para a próxima linha.

Para retirar a numeração de todas as equações de um align ou gather, basta colocar um asterisco na frente do nome desses ambientes.

\begin{gather*} % remove a numeração de todas as equações desse ambiente
  2x + 3y = 16 \\
  x - y = 3
\end{gather*}

\begin{align}
  2x + 3y &= 16\notag \\ % remove a numeração dessa equação
  x - y &= 3
\end{align}